H26年度 神奈川県立高校の入試問題解説 数学の問3(ア)です。
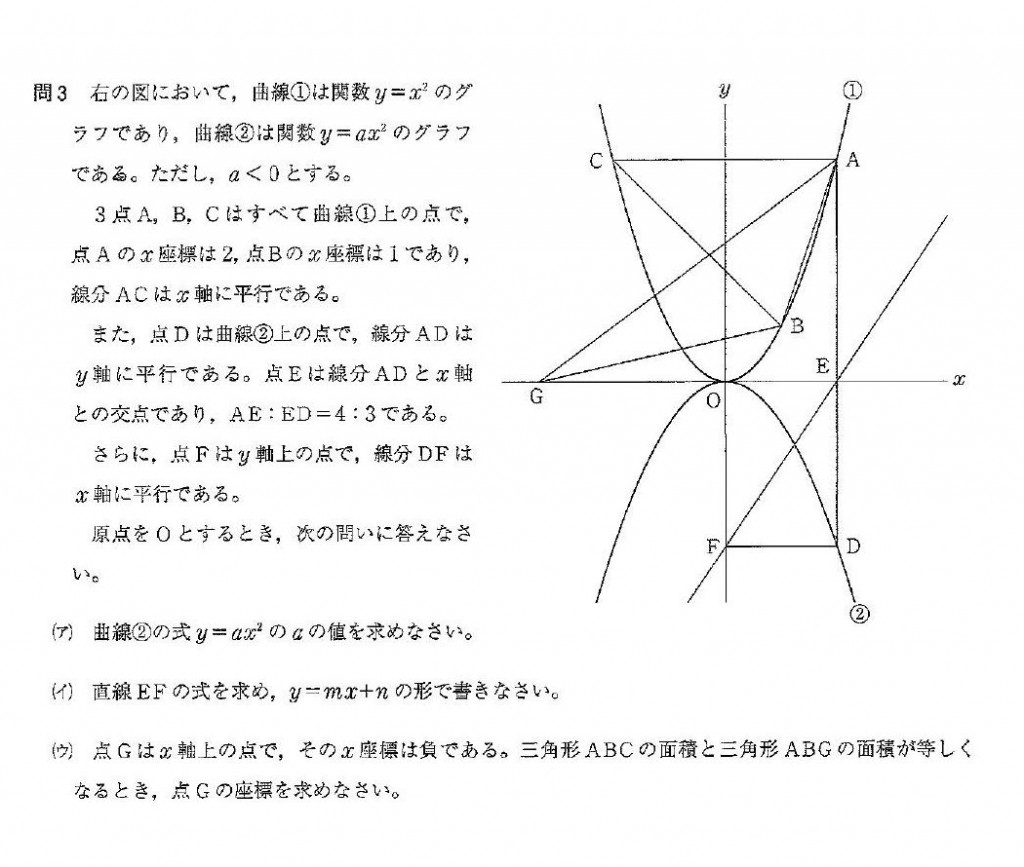
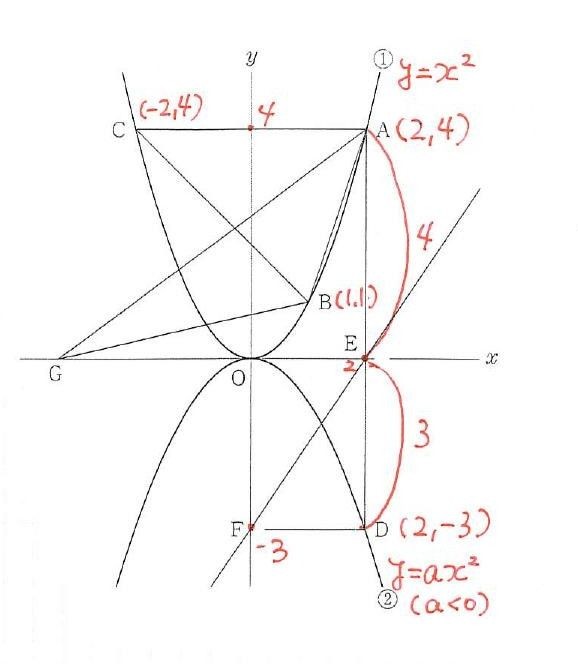
まず、問題文を読みながら分かることを解いていきます。
点Aのx座標は2
→\(y=x^2\) に \(x=2\) を代入すると
\(y=2^2=4\)
したがって、点A\((2,4) \)
点Bの\(x\)座標は1
→\(y=x^2\) に \(x=1\) を代入すると
\(y=1^2=1\)
したがって、点B\((1,1)\)
線分ACは\(x\)軸に平行
→線分ACの式は
\(y=4\)となり、点Aと点Cは\(y\)軸に対して対称だから
点C\((-2,4)\)
線分ADは\(y\)軸に平行
→線分ADの式は
\(x=2\)
したがって、点Dの\(x\)座標は2となるので
点D\((2,4a)\)と表すことができる。
AE:ED=4:3
→点Aの\(y\)座標は4、点Eの\(y\)座標は0なので
\(AE=4\)
したがって、DEの長さは3になるので
点Dの\(y\)座標 4aは-3となる。
\(4a=-3\)
\(a=-\frac{3}{4} \)・・・①
点Fは\(y\)軸上の点で、線分DFは\(x\)軸に平行
→線分DFの式は
\(y=-3\)
また 点F\((0,-3)\)
数学 問3 (ア)
上記①より
\(a=-\frac{3}{4}\)
H26年度 神奈川県立高校 数学入試問題解説
H26年度 神奈川県立高校 数学入試問題解説 問1
H26年度 神奈川県立高校 数学入試問題解説 問2
H26年度 神奈川県立高校 数学入試問題解説 問3(ア)
H26年度 神奈川県立高校 数学入試問題解説 問3(イ)(ウ)
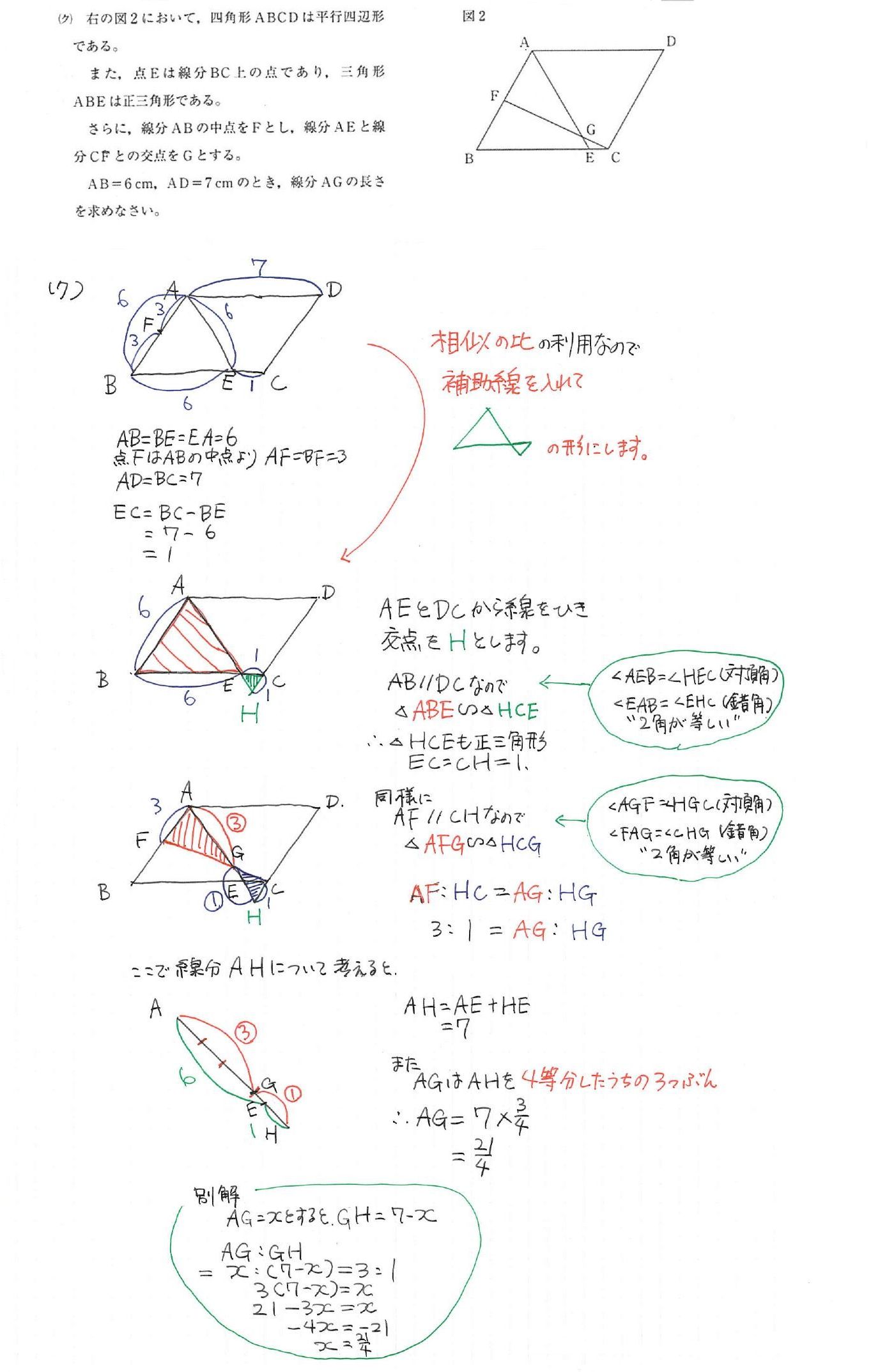

コメント
[…] (ア)で導き出したように、直線EFの\(y\)切片Fの座標は\((0,―3)\)となります。 […]
[…] H26年度 神奈川県立高校 数学入試問題解説 問3(ア) […]
[…] H26年度 神奈川県立高校 数学入試問題解説 問3(ア) […]