比例と反比例 1:式とグラフ

比例と反比例 1:式とグラフ 目次
• 比例と反比例の基本
• 比例と反比例の式
• 比例のグラフ

比例と反比例の基本

• 変数:いろいろな値をとる文字
• 定数:決まった数
• 関数:\(xの値が決まるとyの値も決まるもの\)

	比例	反比例
式	\(y=ax\)	\(\displaystyle y=\frac{a}{x}\)
\(xが2倍,3倍になると\)	\(yも2倍,3倍になる\)	\(\displaystyle yは\frac{1}{2}, \frac{1}{3}になる\)
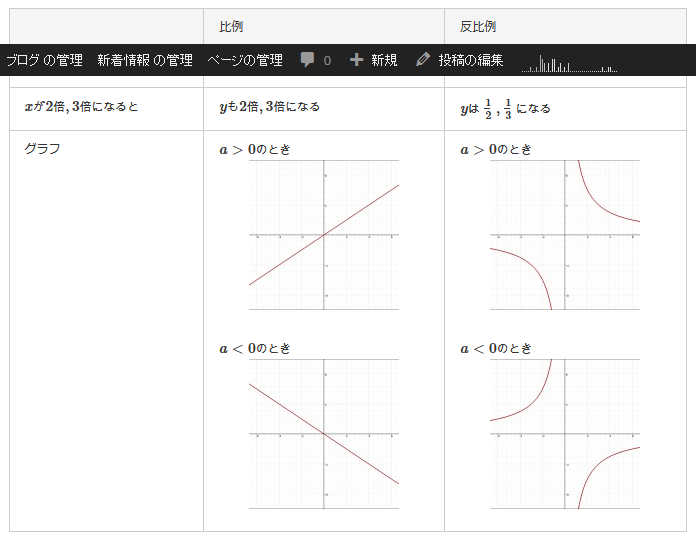
グラフ	\(a>0のとき\)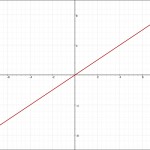 \(a<0のとき\)	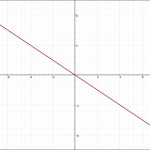\(a>0のとき\)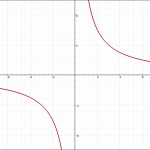 \(a<0のとき\)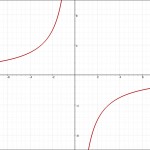

比例と反比例の式

比例の式 \(y=ax\)、反比例の式 \(y=\frac{a}{x}\) の\(a\)の部分を比例定数と言います。
比例定数は整数だけでなく、分数や小数の値をとります。

特に分数のときに間違えやすいので気をつけましょう。

比例定数が分数のとき、\(x\)が分子なら比例、分母なら反比例‼︎

確認
比例の式 \(y=\frac{x}{5}\)と、\(y=\frac{1}{5}x\)は、同じものです。
\(y=\frac{x}{5}\)の比例定数は\(\frac{1}{5}\)になります。

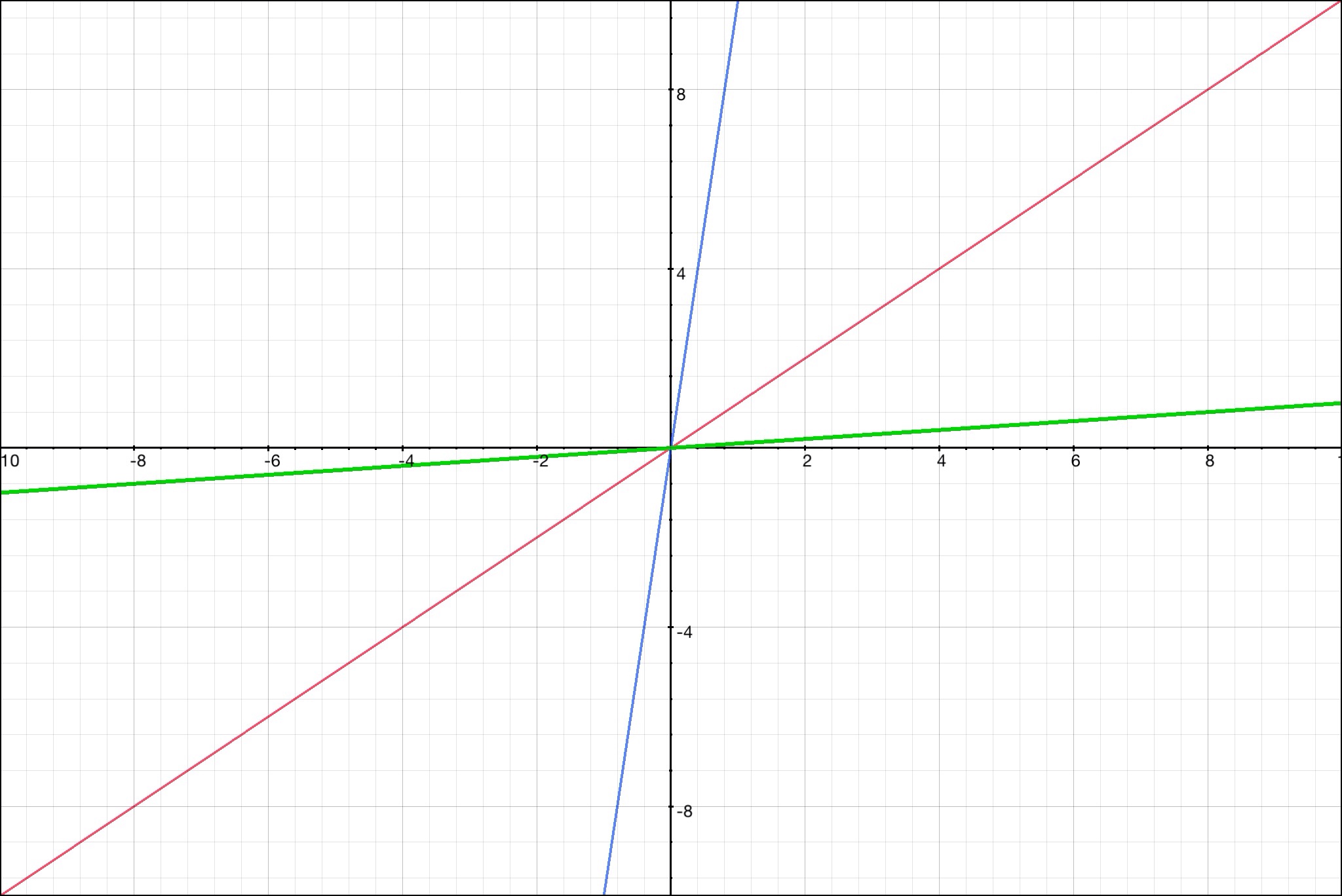
比例のグラフ

比例のグラフは、原点を通る直線

\(a>0のとき (aが正のとき)\)	\(a<0のとき (aが負のとき)\)
右上がり	右下がり
比例定数の値が大きいほど、角度は急になる。	比例定数の値が小さいほど、角度は急になる
\(y=10x\) ,\(y=x\) ,\(y\displaystyle =\frac{1}{10}x\)	\(y=-10x\), \(y=-x\) ,\(\displaystyle y=-\frac{1}{10}x\)

比例定数の絶対値が大きくなれば、角度も急になる。